割合はとどめの単元

小学校の算数程度がわからなくなってしまうなんて人災以外の何物でもありませんから、そんなものは、普通に対策を立てて淡々と実行するのみです。

子どもたちは、本来とても賢いんですから。

割合は「とどめ」の単元だと思っています。絵図で考えれば超簡単な割合を、訳のわからない言葉と公式通りの計算作業を徹底させてわからなくさせてしまう。そのやり方がまずいことをわかっている先生だって少なくない･･･と思いたい。

６年生「割合」の学習　公式の丸暗記でいいの？

富山大学付属小学校教諭

「割合」の学習というと、「公式」が頭に浮かぶ。

①　「割合」＝「比べられる量」÷「もとにする量」

②　「比べられる量」＝「もとにする量」×「割合」

③　「もとにする量」＝「比べられる量」÷「割合」

という３つの「公式」である。

「割合」の学習では、この３つの「公式」を教え込み、そこに数値を当てはめて答えを導き出すという指導が、一般的ではないだろうか。

中には、丸の中に「く」「も」「わ」と書いて公式を覚えさせたり、「『～の』って付いていたら『もとにする量』」と覚えさせたりする指導も見かける。

それでは、意味の分からない公式へ機械的に数値を当てはめるだけの作業になってしまう。

何だか「算数」とは言い難い寂しい風景である。

そもそも、分からない子にとっては、まず、公式に出てくる用語の意味が分からないのである。

試しに若い臨任講師の先生へ次のような実験をしてみた。

『５人のうち２人は男です。男の割合は？』という問題の『比べられる量』って何？と質問したのである。

その若い先生は「『５人』です…よね？」と自信なさげに答えた。

見事にハズレである。彼の名誉のために言えば、彼は決して頭が悪いわけではない。歴とした国立大学を卒業している方である。

もう１つ彼の名誉のために言えば、彼は問題の答えが「５分の２」であることはちゃんと分かっていた。「比べられる量」という用語の意味が分からなかったのである。

国立大学を卒業した大人でさえも用語の意味をとらえづらいのだから、子どもなら、なおさらである。

せっかく公式を覚えても、「比べられる量」が何で、「もとにする量」が何かが分からなければ、公式は使えない。使えないどころか、弊害になる。「関係をとらえること」の難しさに加えて、「用語の意味を理解すること」への負担が増えるのである。

引用元：http://www6.plala.or.jp/maeda-masahide/9kousiki.html

『ある商品を20％引きで買ったら640円でした。定価はいくらでしょうか。』

まず、定価って何？という質問が多い。

次に、もとにする量はどれ？比べられる量は？

あぁ～わかんないになる。

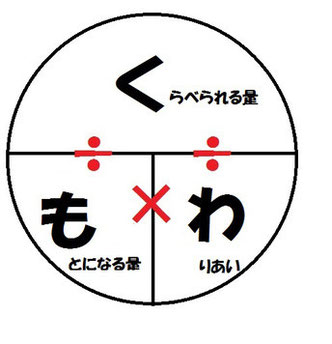
公式を見ながらでもわからない。

640÷0.2＝3200円

640×0.2＝128円

640×20＝12800円

なんてことを普通にやってしまう。

絵図を描けば簡単すぎる問題。

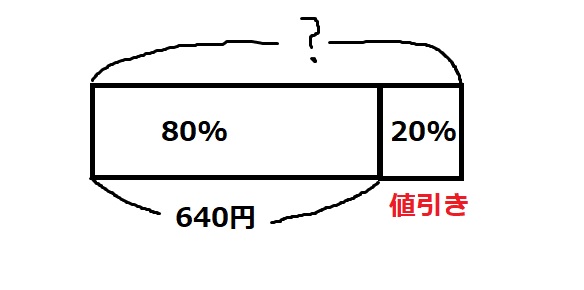
20％引きで640円ということは、定価の80％で買ったってこと。

それが640円だからこんな絵図になる。

知りたいのは100％がいくらか。

80％で640円だから10％で80円、それが10こで800円でもいい。

→640÷8＝80、80×10＝800→640÷80×10＝800

640÷80で1％は8円、1％が100こで100％だから、8×100で800円でもいい。

→640÷80＝8、8×100＝800→640÷80×100＝800

絵図で解いた流れを式にまとめればいい。

教科書のやり方に合わせると･･･□×（1-0.2）＝640、640÷0.8＝800　ですかね。

一つの式にすると、640÷（1-0.2）＝800　か。

いきなり式がたてられる子は何割いるんでしょう？

私もいきなりこの式は立てられません。

なんで簡単な問題をわざわざ難しく解かせるんでしょう？

難しい問題を簡単に解く練習をしたらいいのにと思います。